中学受験の算数において、急激に内容が難しくなる時期があります。四谷大塚予習シリーズで例えるなら「5年下」からとなります。つまり夏休明けから使用するテキストですが、この教材に掲載される内容は中学受験に直結するばかりでなく、6年生に向けたとても大切な分野が盛りだくさんです。
ここを正しく通過できれば6年生になっても大きな苦労はありません。大げさではなく算数については5年生後半が中学受験の天王山だと言えるでしょう。
平面図形
<図形の法則やしくみを学び、利用する>
平面図形を学ぶとき、とにかくはじめはテキストに載っている平面図形をノートに模写してみましょう。テキストに載っているのにわざわざ書き写すわけですから、それだけ意味があり重要なことなのです。
どんな図形が隠れているか・・等しい長さの辺や同じ角度は無いか・・など、自分で模写することでそのヒントを見つける力が養われていきます。
また図形問題を得意にするにはまずは直感と感性を磨く必要があります。公式を使ってそのまま答えが出せるような問題は入試にはほとんど出ません。色々な知識を組み合わせて解いていくのです。公式はあくまでも解答を出す際のツールにすぎず、図形を見て解法までの道筋を論理的に考える思考回路を育てなくてはなりません。中堅クラスの学校では平面図形を求積させる問題が数多く出題されます。仮に志望校に毎年出題されるようであれば、基本的な受験頻出問題100題程度を選び、完璧に正解できるように何度も復習しましょう。コツを覚えればかなりの実力と得点源になるはずです。
| [平面図形の典型問題] |
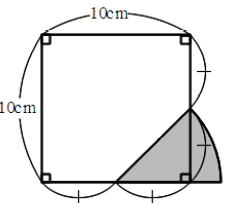 |
例えは上の問題の場合、一見簡単そうに見えますが、平面図形を単に公式だけで解こうと思っても解けません。補助線を自力で書き、二等辺三角形や正方形の別の面積の求め方の知識があれば解けると道筋を立てられるかどうかが分かれ道です。少なくとも中堅クラスの学校を目指す受験生であれば、一見して解けなくてはならない問題です。
四谷大塚の予習シリーズは図形問題の取り扱いがやや少ない傾向があります。補完的な意味合いで市販の問題集で良いものをご紹介しますので、早い段階で平面図形を完成させてしまいましょう。
>>算数図形問題ランキング (日能研ブックス/出題頻度順)
>>中学入試/解き方上手図形問題46回完成(受験研究社)
割合
割合も、その後の学習に密接に繋がるとても大切な分野です。割合の意味をまず教えるところからスタートします。大人は直感で割合を生活で使っていますが、子供にはそういった感覚がありませんので教え方も難しいのです。また新しい言葉もたくさん出てきます。「割」や「歩」、「%」、「原価」「定価」「利益」などもそうです。
割合の基本原理を学んでから次第に相当算や売買算と複雑な分野へと発展させるため、割合の最初の導入は丁寧に教えていきましょう。
いずれの場合でも「くらべる量」と「くらべられる量」の関係であることには変わりありません。
割合の基本が理解できたら相当算をしっかりとやっておきましょう。元の数を「1」として考える問題は、各分野で頻出です。売買算ではことばの意味を、物を仕入れてから販売し利益を得るという一連の流れから理解させます。
また割合の問題では文章の読解力がポイントとなる場合があります。「〜に対する」や「〜の」などの表現に注意しなければなりません。
売買算では特に線分図が活躍しますので、線分図が自力で書けるようにすることもポイントとなります。
[割合の典型問題]
A君は本を読み始めましたが、1日目に全体の1/3を読み、2日目に残りの2/5を読んだとろこ78ページが残りました。この時2日目に読んだのは( )ページです。またこの本は全部で( )ページあります。
これも基本問題として何度となく出現する受験の典型問題です。ポイントは2本の線分図をしっかり書いて提示されている条件を整理するところから解法の道筋を立てます。
>>算数は「図」で考えればグングン伸びる!―中学受験で驚異の合格実績
>>算数解法マスター(中学入試百点満点 究極の受験算数のすべての問題を徹底的に)
規則性
文章を図や表にして考えたり、さらにその表の先はどうなっていくのかを調査したりします。その表を元にどういった規則で数字が並んでいるか、隠されたところを推理していきます。
図を描く時は、大きくはっきりと描きます。そしてその図の中に判っていることをどんどん書き込んでいきましょう。また図を描く時は、縦の線や横の線が何を示しているのかをしっかりと頭で意識しながら描き始めます。そうしなければ正しい図にならないからです。
表を書く時は単に数字を並べていくのではなく、規則性を意識して書いてみましょう。「3の倍数ずつ増えている」とか「1.3.5.7」の周期になっているとかです。また入試では横に並んだ数値を縦に規則性を持たせていたり、斜めであったりとあらゆる角度から観察することが必要となります。
規則性は「解き方」をいくら覚えても対応できません。全く同じ問題が出題されるならともかく、規則を見つけ出せる力が無ければ解けないため、苦手とする受験生も多いのが現状です。まさに「習うより慣れろ」です。志望校に毎年出題されるようであれば他の分野より、多くの問題を解いておく必要がありますが、苦手な受験生が多いとはいえ、難問奇問は少ないため得意分野にしてしまえば、有効な得点源となりえる分野でもあります。
等差数列ではいくつかの公式があります。
S番目の数を求める
・はじめの数 + 等差 × (Sー1)
等差数列の個数を求める
・(終わりの数 − はじめの数) ÷ 等差 + 1
等差数列の和
・(はじめの数 + 終わりの数) × 数の個数 ÷ 2
公式に当てはめて機械的に解くのは6年生になってから。5年生ではまずこの公式の意味をしっかりと教えましょう。「どうして最後に1を足すのか」「どうして最後に2で割るのか」などです。等差数列のみを解いているうちは良いのですが、等比数列をやりだすと公式を間違えやすくなります。
[等差数列の典型問題]
○・・・・・・・・・・・・・・・・・・・・1段目
○○○・・・・・・・・・・・・・・・・2段目
○○○○○
○○○○○○○
49段目は○がいくつ並んでいますか?またその時に全ての○はいくつになりますか?
まさか・・49段目まで地道に○を書いて解こうとする受験生はいないと思います。
| << 次へ (比・速さ・立体図形) |
中学受験 スポンサーサイト